The Ultimate GCSE & A-level maths platform.
Free and comprehensive digital maths textbooks with all the tools you need in one place. Zero ads. Zero distractions.
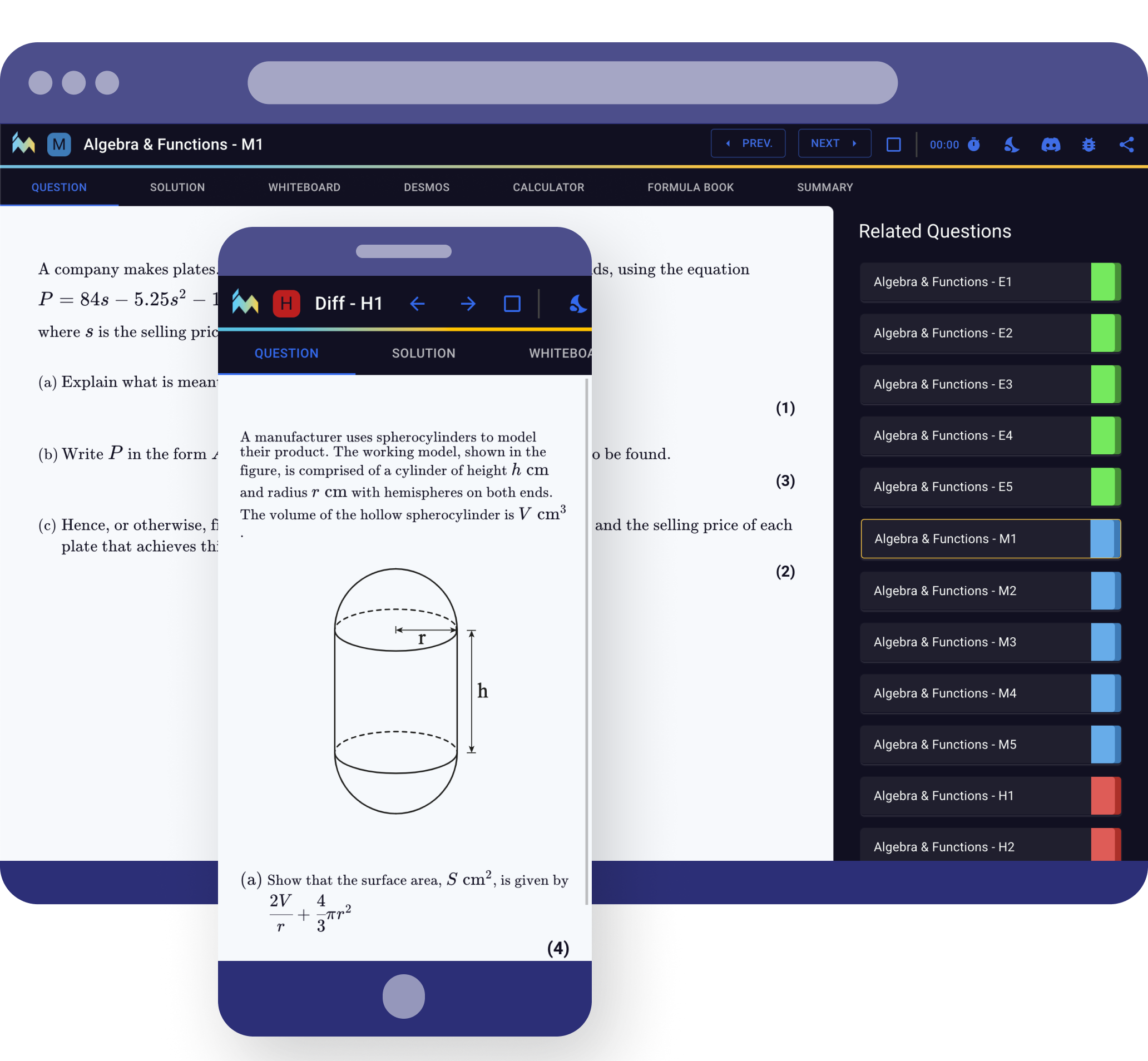

What's included?
Comprehensive content
Our textbooks have you covered on both theory and practice worksheets for a range of relevant subtopics.
Practice Papers
Our original practice papers give you extra material with handcrafted questions.
Personalised AI Tutor
Get help on demand with your own personalised AI tutor.
Comprehensive content
Our textbooks have you covered on both theory and practice worksheets for a range of relevant subtopics.
Practice Papers
Our original practice papers give you extra material with handcrafted questions.
Personalised AI Tutor
Get help on demand with your own personalised AI tutor.
Videos that bring maths to life
Our textbooks are packed with animated videos that make mathematical concepts easier to visualise.
Community
Chat to us directly on Discord
Learning is easier when you're learning with others. Connect with other GCSE & A-level students on our free discord server.


Chat to us directly on Discord
Learning is easier when you're learning with others. Connect with other GCSE & A-level students on our free discord server.
Mini-papers
Mini-papers are a collection of short and interesting mathematical results.
How many combinations does a rubix cube have?

Novica Petrovic
Does the sun really transmit our annual energy needs in 1 hour?

Novica Petrovic
Deriving the age of the universe
